WRF
Entwicklung
Das Weather Research and Forecasting WRF Model (Skamarock et al., 2005, 2008, 2021) wurde gemeinsam vom National Center for Atmospheric Research (NCAR), der National Oceanic and Atmospheric Administration (NOAA), der Air Force Weather Agency (AFWA), dem Naval Research Laboratory, der University of Oklahoma, und der Federal Aviation Administration (FAA) in den USA entwickelt. WRF ist ein mesoskaliges numerisches Wettervorhersagemodell, das so entwickelt wurde, dass es sowohl den Ansprüchen operationeller Wettervorhersage, regionaler Klimasimulationen als auch atmosphärischer Forschung gerecht wird. Die WRF Softwareumgebung unterstützt 2 dynamische Kerne: das Advanced Research WRF (ARW), das am NCAR entwickelt und gepflegt wird, und das WRF Nonhydrostatic Mesoscale Model (WRF-NMM) das von den National Centers for Environmental Prediction (NCEP) und NOAA entwickelt wird. WRF wird für Anwendungen mit Gitterauflösungen von 10 m bis 50 km angewendet, dabei lassen sich Gebiete mit hoher Auflösung in die Gebiete gröberer Auflösung einbetten und entweder gleichzeitig oder nacheinander rechnen. Für die Anwendung kann vom Anwender aus einer Vielzahl von Parametrisierungen und Projektionen eine geeignete Konfiguration zusammengestellt werden. In der Klima- und Wetterforschung kommt vor allem das WRF-ARW zum Einsatz, das im Weiteren basierend auf Skamarock et al. (2008 und 2021) beschrieben wird. Details finden sich auf der WRF-Homepage, die regelmäßig aktualisiert wird.
WRF-Homepage
Atmosphärische Dynamik und Modellkonfiguration
Bei WRF handelt es sich um ein kompressibles nichthydrostatisches Modell. Für alle skalaren Größen gelten die Erhaltungsgleichungen. Es besteht die Möglichkeit, das WRF hydrostatisch anzuwenden. Das Modell beinhaltet die prognostischen Variablen Windgeschwindigkeit (u,v,w) sowie Störungen in potentieller Temperatur, Geopotential und Oberflächendruck.
Optional können turbulente kinetische Energie und eine Vielzahl skalarer Größen (z.B. Mischungsverhältnisse) ausgegeben werden. WRF wird auf einem Arakawa C-Gitter mit geländefolgenden hybriden Sigma-Druckkoordinaten betrieben (Park et al., 2013).
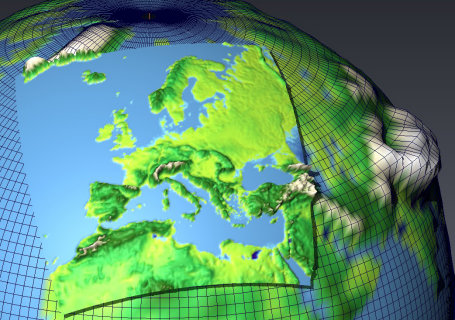
Die zeitliche Integration erfolgt mit einem Runge-Kutta-Schema 2. bzw. 3. Ordnung. WRF kann in verschiedenen Projektionen betrieben werden, z.B. Lambert conformal, Mercator, und Gradnetz (auch mit rotiertem Pol). Verschiedene horizontale Gitter können ineinander geschachtelt werden: mit Wechselwirkung in einer Richtung, in zwei Richtungen und mit sich bewegenden Gebieten (z.B. bei Hurrikan-Simulationen) (Abb. 1).
WRF bietet die Wahl aus einer Vielzahl von Optionen für die Modellphysik. So gibt es z.B. verschiedene Optionen für die Mikrophysik, Landoberflächenmodelle, Grenzschicht-Schemata und Konvektionsparametrisierungen unterschiedlicher Komplexität.
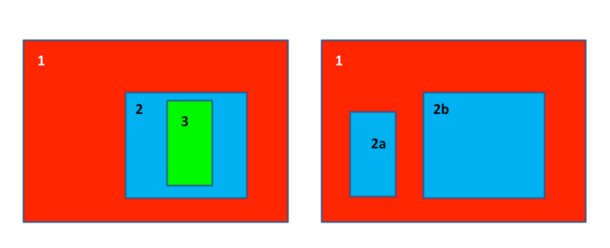
Abb. 1: Verschiedene horizontale Gitter können ineinander geschachtelt werden, hier hat Gebiet 3 die feinste, Gebiet 1 die gröbste horizontale Auflösung.
Das ganze WRF-System (Abb. 2) beinhaltet neben dem eigentlichen WRF-Modell auch ein Vorbereitungspaket (WRF-Preprocessing System (WPS)) als auch ein Paket zur Aufbereitung der Ergebnisse (WRF-Postprocessing Package (WPP)). Die Aufgabe des WPS ist es, meteorologische Antriebsdaten und terrestrische Daten aufzunehmen, Initialisierungsfelder zu erzeugen und alle Daten für den geplanten Modelllauf zu formatieren. Das WRF-Modell besteht aus digitalen Filtern, die Hintergrundrauschen aus den Eingabedaten entfernen, dem dynamischen Kern (WRF-ARW oder WRF-NMM) zur 3-dimensionalen Lösung der atmosphärischen Strömungsdynamik, den physikalischen Parameterisierungen (s.u.) subskaliger Prozesse und dem Austauschmodul für physikalische Größen zwischen Parameterisierungen und dynamischem Kern. Optional ist die zusätzliche Verwendung der variationellen Datenassimilation (WRF-VAR) oder eines Modells für Atmosphärenchemie (WRF-Chem).
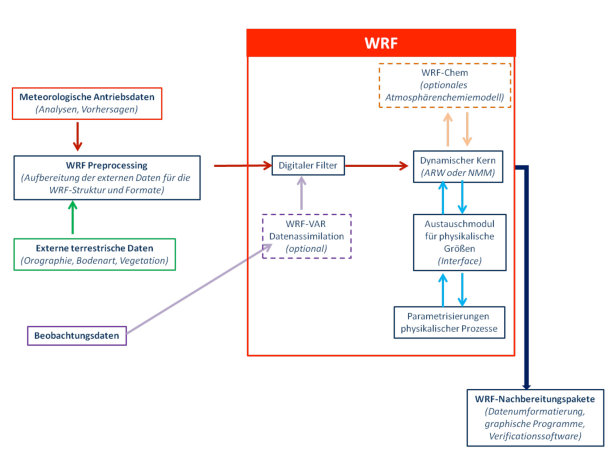
Abb. 2: Flussdiagramm des WRF-Systems (nach Skamarock et al., 2008)
Physikalische Parametrisierungen
Subskalige Prozesse werden mit Hilfe von Parameterisierungen (z.B. Mikrophysik) oder Säulenmodellen (z.B. Landoberflächenmodelle) berechnet. Dabei sind die Parameterisierungen nicht unabhängig voneinander und tauschen Größen wie z.B. Temperatur, Feuchte und Niederschlag aus.
Die Mikrophysik beinhaltet die explizite Auflösung der Prozesse, die die Bildung von Wasserdampf, Wolken und Niederschlag beschreiben. Es kann hier aus einer Vielzahl von Modellen unterschiedlicher Komplexität gewählt werden, z.B. dem Kessler-Schema (Kessler, 1969), dem Thompsen et al. -Schema (Thompsen et al. 2004) und dem Morrison et al. -2-Momenten-Schema (Morrison et al., 2008). Auch Aerosole werden z.T. inzwischen berücksichtigt (z.B. Thompson und Eidhammer 2014).
Die Konvektionsparametrisierungen werden zur Erfassung subskaliger Effekte von konvektiven und/oder flachen Wolken benötigt (d.h. wenn die horizontale Auflösung > 4km ist). Diese Schemata sollen die vertikalen Flüsse durch nicht vom Modell aufgelöste Vertikalbewegungen darstellen. Für die Konvektionsparametrisierung stehen u.a. ein modifiziertes Kain-Fritsch-Schema (Kain, 2004), ein neues Tiedke-Schema (Zhang und Wang 2017) und das Grell- Freitas-Schema (Grell und Freitas 2014) zur Verfügung.
Die Prandtl-Schicht ist die unterste Schicht der Atmosphärischen Grenzschicht. Sie beträgt in etwa 10% der Atmosphärischen Grenzschicht. Die turbulenten Austauschkoeffizienten für Wärme, Feuchte und Impuls in der Prandtl-Schicht werden in WRF mit dem sog. Oberflächenschichtschema berechnet. Hier stehen Parametrisierungen zur Wahl, welche auf der Monin-Obukkhov-Theorie (Monin und Obukhov, 1954) und Stabilitätsfunktionen basieren. Häufig wird die Parametrisierung von Jiminez et al. (2012) verwendet. Allerdings ist die Prandtl-Schicht ist das Bindeglied zwischen der Landoberfläche und der planetarischen Grenzschicht (s.u.), d. h. die Wahl muss zum ausgewählten Grenzschichtschema und Landoberflächenmodell passen.
Die Wasser- und Energieflüsse an der Landoberfläche, d.h. im Boden, in der Vegetation und zwischen Boden, Vegetation und atmosphärischer Grenzschicht werden durch Landoberflächenmodelle berechnet, die mit WRF gekoppelt sind. Es besteht die Auswahl zwischen sehr unterschiedlichen Modellen, von denen das NOAH (Chen and Dudhia, 2001) mit der Möglichkeit einer Heterogenität der Vegetation in Gitterzellen (Li et al., 2013) und seit WRF Version 3.4 das NOAH-MP (Niu et al., 2011) die größte Komplexität aufweisen. Inzwischen beinhaltet Noah-MP im WRF auch zwei Getreidewachstumsmodelle (Liu et al. 2016, Warrach-Sagi et al. 2022).
Die Parametrisierung der planetarischen Grenzschicht (PBL) ist für die vertikalen subskaligen turbulenten Flüsse in der gesamten atmosphärischen Säule oberhalb der Prandtl-Schicht verantwortlich. Wird ein PBL- Schema in WRF aktiviert, so wird die vertikale Diffusion deaktiviert, da das PBL diese beinhaltet. Die Oberflächenflüsse werden vom Oberflächenschichtschema und dem Landoberflächenmodell zur Verfügung gestellt. Das PBL Schema bestimmt daraus die Flussprofile in der gut durchmischten Grenzschicht und der stabilen Schicht und berechnet so die atmosphärischen Tendenzen für Temperatur, Feuchte (inklusive Wolken) und horizontalen Impuls in der gesamten atmosphärischen Säule. Die PBL Schemata sind eindimensional und nehmen an, dass es eine klare Trennung zwischen subskaligen und vom Modell aufgelösten Wirbeln gibt. Zur Auswahl stehen verschiedene PBL Schemata, z.B. das Yonsei University (YSU) (Hong et al. 2006), das Mellor-Yamada-Janjic (MYJ) (Janjic 1990, 2002, Mellor and Yamada 1982) und das auf turbulenter kinetischer Energie basierende Mellor-Yamada-Nakanishi-Niino (MYNN) (Nakanishi und Niino 2006, 2009, Olson 2019) PBL Schema.
Mit Hilfe von Strahlungstransportmodellen wird die kurzwellige und langwellige Strahlung berechnet. Es kann zwischen ca. 5 Modellen gewählt werden, die unterschiedliche Spektralbänder unterscheiden und unterschiedlich komplex sind, z.B. das aus dem NCAR Community Atmosphere Model (CAM 3.0) stammende Schema für Klimasimulationen. Es kann die optischen Eigenschaften verschiedener Spurengase bzw. Aerosole berücksichtigen und wechselwirkt mit im Modell aufgelösten Wolken. Das CAM-Strahlungsschema ist in Collins et al. (2004) dokumentiert. Ein weiteres Strahlungstransportmodell für die langwellige Strahlung in WRF ist das Rapid Radiative Transfer Model for GCMs (RRTMG) (Iacono et al. 2008) das die Effekte von Wasserdampf, Ozon, CO2, Spurengasen und Wolken berücksichtigt.
Ausgabegrößen
Standardmäßig werden in WRF sämtliche berechnete atmosphärischen und Landoberflächenvariablen in NetCDF ausgegeben, eine Liste findet sich z.B. in der Dokumentation von WRF (Skamarock et al., 2008). Ein Umwandlungsprogramm erlaubt die Konvertierung in CF-konformes NetCDF Format, so dass die Ergebnisse mit den CDOs (Climate Data Operators) bearbeitet werden können.
Dr. Kirsten Warrach-Sagi
Institut für Physik und Meteorologie,
Universität Hohenheim
kirsten.warrach-sagi[at]uni-hohenheim.de
- Chen, F., and J. Dudhia, 2001: Coupling an advanced land-surface/ hydrology model with the Penn State/ NCAR MM5 modeling system. Part I: Model description and implementation. Mon. Wea. Rev., 129, 569–585
- Collins, W.D. et al., 2004: Description of the NCAR Community Atmosphere Model (CAM 3.0), NCAR Technical Note, NCAR/TN-464+STR, 226pp. 105
- Hong, S.-Y., and Y. Noh, and J. Dudhia, 2006: A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Wea. Rev., 134, 2318–2341
- Janjic, Z. I., 1990: The step-mountain coordinate: physical package, Mon. Wea. Rev., 118, 1429–1443
- Janjic, Z. I., 1994: The step-mountain eta coordinate model: further developments of the convection, viscous sublayer and turbulence closure schemes, Mon. Wea. Rev., 122, 927–945
- Cooper, W. A., 1986: Ice initiation in natural clouds. Precipitation Enhancement — A Scientific Challenge, Meteor. Monogr., No. 43, Amer. Met. Soc., 29–32.
- Grell, G. A. and Freitas, S. R., 2014: A scale and aerosol aware stochastic convective parameterization for weather and air quality modeling. Atmos. Chem. Phys., 14, 5233-5250, doi:10.5194/acp-14-5233-2014.
- Hong, S.-Y., and Y. Noh, and J. Dudhia, 2006: A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Wea. Rev., 134, 2318–2341.
- Iacono, M. J., J. S. Delamere, E. J. Mlawer, M. W. Shephard, S. A. Clough, and W. D. Collins, 2008: Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res., 113, D13103.
- Janjic, Z. I., 2002: Nonsingular Implementation of the Mellor–Yamada Level 2.5 Scheme in the NCEP Meso model, NCEP Office Note, No. 437, 61 pp. 107
- Jimenez, P., J. Dudhia, J. F. Gonzalez-Ruoco, J. Navarro, J. P. Montavez, and E. Garcia-Bustamente, 2012: A revised scheme for the WRF surface layer formulation. Mon. Wea.Rev., 140, 898–918.
- Kain, J. S., 2004: The Kain-Fritsch convective parameterization: An update. J. Appl. Meteor., 43, 170–181
- Kessler, E., 1969: On the distribution and continuity of water substance in atmospheric circulation, Meteor. Monogr., 32, Amer. Meteor. Soc., 84 pp
- Li, D., E. Bou-Zeid, M. Barlage, F. Chen, and J. A. Smith, 2013: Development and Evaluation of a Mosaic Approach in the WRF-Noah Framework. J. Geophys. Res., 118, 11918–11935.
- Liu, X., Chen, F., Barlage, M., Zhou, G., & Niyogi, D. (2016). Noah‐MP‐Crop: Introducing dynamic crop growth in the Noah‐MP land surface model. Journal of Geophysical Research: Atmospheres, 121(23), 13-953.
- Mellor, G. L., and T. Yamada, 1982: Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. Space Phys., 20, 851–875
- Monin, A.S. and A.M. Obukhov, 1954: Basic laws of turbulent mixing in the surface layer of the atmosphere. Contrib. Geophys. Inst. Acad. Sci., USSR, (151), 163–187 (in Russian and English)
- Morrison, H., G. Thompson, and V. Tatarskii, 2008: Impact of cloud micrpohysics on the development of trailing stratiform precipitation in a simulated squall line: Comparison of one- and two-moment schemes. Submitted to Mon. Wea. Rev. https://doi.org/10.1175/2008MWR2556.1.
- Nakanishi, M., and H. Niino, 2006: An improved Mellor-Yamada level 3 model: its numerical stability and application to a regional prediction of advecting fog. Bound. Layer Meteor., 119, 397–407.
- Nakanishi, M., and H. Niino, 2009: Development of an improved turbulence closure model for the atmospheric boundary layer. J. Meteor. Soc. Japan, 87, 895–912.
- Niu, G.-Y., et al. (2011), The community Noah land surface model with multipara-meterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements, J. Geophys. Res., 116, D12109, doi:10.1029/2010JD015139
- Olson, J. B., J. S. Kenyon, W.. A. Angevine, J. M. Brown, M. Pagowski, and K. Suˇselj, 2019: A Description of the MYNN-EDMF Scheme and the Coupling to Other Components in WRF-ARW. NOAA Technical Memorandum.
- Park, S.-H., W. Skamarock, J. Klemp, L. Fowler, and M. Duda, 2013: Evaluation of global atmospheric solvers using extensions of the Jablonowski and Williamson baroclinic wave test case. Mon. Wea. Rev., 141, 3116–3129.
- Skamarock, W. C., J. B. Klemp, J. Dudhia, D. O. Gill, D. M. Barker, M. Duda, X.-Y. Huang, W. Wang and J. G. Powers, 2008: A Description of the Advanced Research WRF Version 3. NCAR Technical Note, 2008
- Skamarock, W. C., Klemp, J. B., Dudhia, J., Gill, D. O., Liu, Z., Berner, J., … Huang, X. -yu. (2021). A Description of the Advanced Research WRF Model Version 4.3 (No. NCAR/TN-556+STR). doi:10.5065/1dfh-6p97
- Thompson, G., and T. Eidhammer, 2014: A study of aerosol impacts on clouds and precipitation development in a large winter cyclone. J. Atmos. Sci., 71, 3636–3658.
- Thompson, G., R. M. Rasmussen, and K. Manning, 2004: Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part I: Description and sensitivity analysis. Mon. Wea. Rev., 132, 519–542
- Warrach-Sagi, K., J. Ingwersen, T. Schwitalla, C. Troost, J. Aurbacher, L. Jach, T. Berger, T. Streck, and V. Wulfmeyer, 2022: Noah-MP with the generic crop growth model Gecros in the WRF model: Effects of dynamic crop growth on land-atmosphere interaction. J Geophys Res-Atmos, 127(14), e2022JD036518. DOI:10.1029/2022JD036518
- Zhang, C. and Y. Wang, 2017: Projected Future Changes of Tropical Cyclone Activity over the Western North and South Pacific in a 20-km-Mesh Regional Climate Model. J. Climate, 30, 5923-5941. doi:10.1175/JCLI-D-16-0597.1.