HIRHAM-NAOSIM
Das regionale Klimamodell HIRHAM-NAOSIM (Rinke et al., 2003; Dorn et al., 2007, 2009, 2012; Rinke et al., 2013) ist ein gekoppeltes Atmosphären-Ozean-Meereis-Modell für die Arktis. Es besteht aus dem regionalen atmosphärischen Klimamodell HIRHAM (Christensen et al., 1996; Dethloff et al., 1996) und dem regionalen Ozean-Meereis-Modell NAOSIM (Köberle und Gerdes, 2007).
Modellkomponenten
HIRHAM ist ein dreidimensionales atmosphärisches Zirkulationsmodell, welches auf die Arktis angewendet wird. HIRHAM basiert auf dem numerischen Wettervorhersagemodell der skandinavischen Länder HIRLAM (High-Resolution Limited Area Model; Machenhauer, 1988; Gustafsson, 1993) und enthält die physikalischen Parametrisierungen des globalen Zirkulationsmodells ECHAM4 (Roeckner et al., 1996). Daher ist HIRHAM dem unter 2.1.2 beschriebenen REMO sehr ähnlich. Aktuell wurden die Parametrisierungen des Nachfolgemodells ECHAM5 (Roeckner et al., 2003) in HIRHAM implementiert. HIRHAM enthält neben der atmosphärischen Modellkomponente auch ein Landoberflächen-Boden-Modell, um die thermischen und hydrologischen Prozesse im arktischen Permafrostboden zu simulieren (Rinke et al., 2008; Matthes et al., 2011).
Das Modellgebiet umfasst die gesamte Arktis, d.h. das Gebiet nördlich von ~60°N (Abbildung 1). Im gekoppelten Modus wird HIRHAM mit einer horizontalen Auflösung von 0.5° (~50 km) und einem Zeitschritt von 240 s (4 Minuten) gerechnet.
HIRHAM berechnet die prognostischen Größen Lufttemperatur, horizontale Windkomponenten, spezifische Feuchte, Wolkenwasser, Bodenluftdruck und viele diagnostische meteorologische Größen (z.B. Strahlung, Niederschlag, usw.) und verschiedene Erdbodenparameter (z.B. Schneedicke, Bodentemperaturen, usw.) (siehe Kapitel REMO).
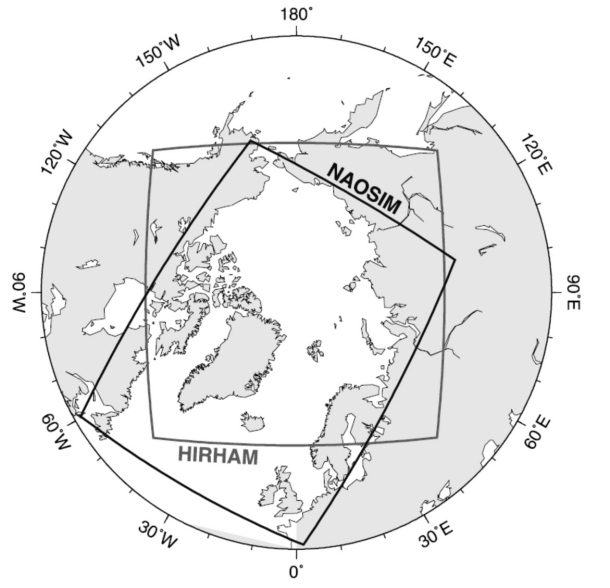
Abbildung 1: Integrationsgebiete des atmosphärischen Regionalmodells HIRHAM und des angekoppelten regionalen Ozean-Meereismodells NAOSIM.
NAOSIM ist ein gekoppeltes Ozean-Meereismodell (North Atlantic/Arctic Ocean-Sea Ice Model) für den nördlichen Nordatlantik und den Arktischen Ozean. Die ozeanische Modellkomponente basiert auf dem Modularen Ozeanmodell MOM-2 (Pacanowski, 1996) und berechnet die dreidimensionale Zirkulation des Ozeans, d.h. horizontale Transporte (Advektion und Diffusion) und vertikale Konvektion. Das dynamisch-thermodynamische Meereismodell (Lemke et al., 1997) berechnet sowohl die Dynamik des Meereises (Eisbewegung und -deformation) mit Hilfe eines elastisch-viskos-plastischen (EVP) Modells [1] (Hunke und Dunkowicz, 1997) als auch thermodynamische Prozesse durch Gefrieren und Schmelzen des Meereises (Semtner, 1976; Hibler, 1979).
Das Modellgebiet umfasst den nördlichen Nordatlantik, das Europäische Nordmeer und den Arktischen Ozean (Abbildung 1). Im gekoppelten Modus wird NAOSIM mit einer horizontalen Auflösung von 0.25° (~25 km) und einem Zeitschritt von 900 s (15 Minuten) gerechnet.
NAOSIM berechnet die prognostischen Größen Ozeantemperatur, horizontale Ozeanströmungen, ozeanischer Salzgehalt, Meereisbedeckungsgrad [2], –dicke und -driftgeschwindigkeit, Schneedicke auf Meereis und viele diagnostische Größen im Ozean (z.B. Vertikalgeschwindigkeit, Wasserdichte, Wärmetransporte, usw.).
[1] In der Gleichung für die horizontale Eisdriftgeschwindigkeit müssen die durch die Wechselwirkung der einzelnen Eisschollen verursachten internen Kräfte beschrieben werden. Es gibt verschiedene Ansätze, wie die internen Spannungen von der Deformation abhängen. Ein EVP Modell beschreibt das Meereis als kontinuumsmechanisches Medium, welches durch Kompressions- und Scherkräfte verformt werden kann. Dabei wird dem Meereis sowohl plastisches (Deformation erst bei Überschreitung einer Grenzspannung) als auch elastisch-viskoses (Spannung proportional zur Deformation) Materialverhalten zugeschrieben.
[2] Der Meereisbedeckungsgrad (bzw. die Meereiskonzentration) gibt den Anteil der eisbedeckten Fläche pro Gitterzelle an und kann zwischen 0% (komplett eisfreie Gitterzelle) und 100% (geschlossene Eisbedeckung in der Gitterzelle) schwanken.
Modellkopplung
Das Atmosphärenmodell berechnet die Flüsse von Wärme (kurz- und langwellige Strahlung, turbulenter Wärmefluss), Feuchte (Niederschlag, Verdunstung) und Impuls (Windschub) und gibt diese ans Ozean-Meereismodell. Im Gegenzug liefert das Ozean-Meereismodell die Zustandsgrößen (Meeresoberflächentemperatur und -Salzgehalt, Meereisdicke, usw.) zur Berechnung der Flüsse (Abbildung 2).
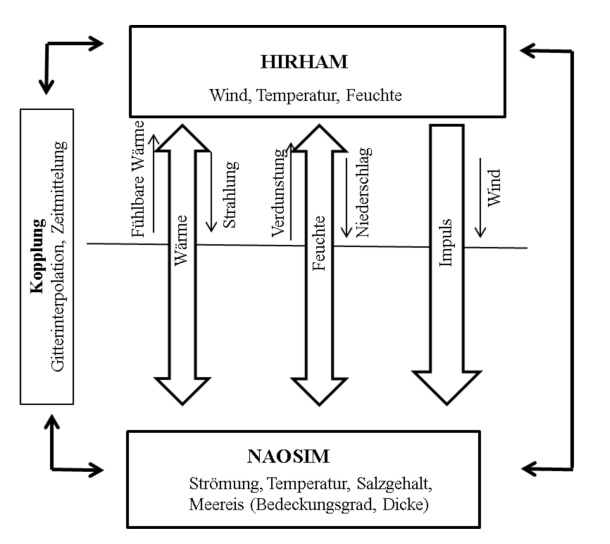
Abbildung 2: Schema der Kopplung des Atmosphärenmodells HIRHAM mit dem Ozean-Meereismodell NAOSIM.
Die Kopplung zwischen HIRHAM und NAOSIM wird jede Stunde durchgeführt. Da HIRHAM und NAOSIM verschiedene Modellgitter und eine verschiedene horizontale Auflösung haben, müssen die Austauschgrößen von einem zum anderen Gitter interpoliert werden. Die Kopplung zwischen Atmosphäre und Ozean-Meereis wird konkret über den Austausch von verschiedenen Modellvariablen realisiert (Abbildung 3).
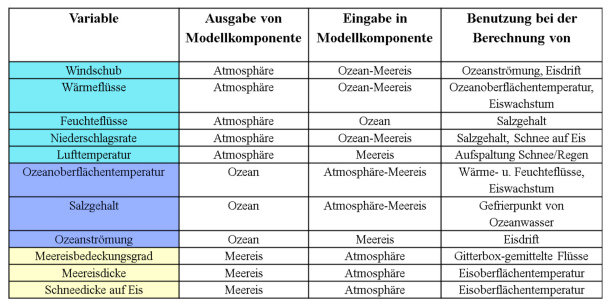
Abbildung 3: Liste der Austauschvariablen von der Atmosphäre (hellblau), Ozean (dunkelblau) und Meereis (gelb), welche während der Kopplung zwischen Atmosphäre und Ozean-Meereis übergeben werden (nach Dorn et al., 2007).
Anwendungsbeispiel
Das gekoppelte Regionalmodell HIRHAM-NAOSIM wurde auf die Arktis angewendet und für den Zeitraum 1948-2008 gerechnet (Dorn et al., 2012). Dabei wurde das Modell an seinen seitlichen Rändern mit den NCEP/NCAR-Reanalysedaten (Kalnay et al., 1996) angetrieben. Es wurden nicht nur eine Simulation, sondern sieben Simulationen über diese 61 Jahre durchgeführt. Diese Simulationen wurden jeweils mit einem anderen Anfangszustand [3] der Ozean- und Meereisgrößen gestartet, um zu berücksichtigen, dass man den wirklichen Zustand des arktischen Ozeans in den 1940er Jahren nicht genau kennt.
[3] Die Felder der Ozean- und Meereisgrößen entsprechen einem bestimmten Jahr (z.B. 1.1.1955 oder 1.1.1956) einer zuvor durchgeführten Simulation zum Einschwingen des Modells.
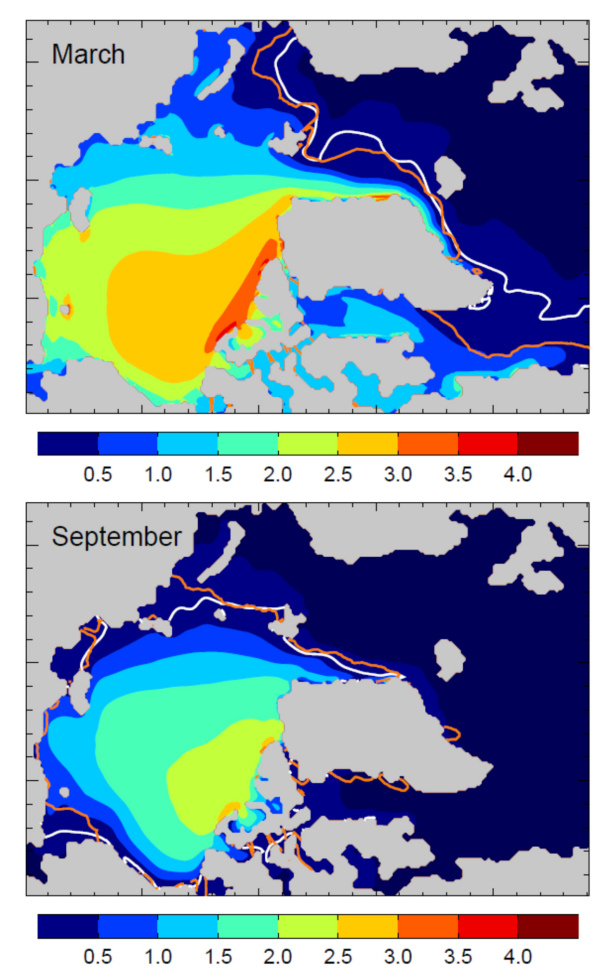
Abbildung 4: Simulierte mittlere arktische Meereisausdehnung (weiße Linien) und Meereisdicke (farbige Kontouren; Einheit: Meter) für März (Monat mit maximaler Eisbedeckung) und September (Monat mit minimaler Eisbedeckung). Die Modellergebnisse sind Ensemblemittel von 7 Simulationen. Die orange Linien zeigen die mittlere Meereisausdehnung basierend auf den NCEP/NCAR-Reanalysedaten. Die Grafik basiert auf Daten der Zeitperiode 1948-2008 (Dorn et al., 2012).
Abbildung 4 zeigt die simulierten mittleren arktischen Meereisbedingungen für März, den Monat mit der maximalen Eisbedeckung, und für September, den Monat mit minimaler Eisbedeckung. Die simulierte Verteilung des dicken und dünnen Meereises entspricht dem was man von Beobachtungen weiß: Man findet das mehrjährige, dicke Meereis nördlich des kanadischen Archipels, welches im März im Mittel mehr als 3 m dick ist, während das dünne Meereis in den sibirischen Schelfgebieten zu finden ist. Die simulierte Meereisausdehnung zeigt eine gute Übereinstimmung mit den Beobachtungen, hat aber auch Defizite. Im März überschätzt das Modell die Eisbedeckung insbesondere in der Labradorsee. Der Grund ist noch unklar, denn dieses Defizit zeigt sich nicht in dem ungekoppelten Ozean-Meereismodell NAOSIM. Das deutet darauf hin, dass dieser Fehler im gekoppelten HIRHAM-NAOSIM vermutlich durch einen falsch wiedergegebenen Rückkopplungsprozess zwischen den Teilmodellen entsteht. Im September überschätzt das Modell die Eisbedeckung in der Beaufortsee, was möglicherweise durch im Modell fehlenden Transport von warmem Wasser durch die Beringstraße in die Arktis zustande kommt.
Mehrwert durch Kopplung
Bevor man beide Modelle HIRHAM und NAOSIM miteinander gekoppelt hat, wurden (bzw. werden) beide Modelle autonom, d.h. ungekoppelt als sogen. „stand-alone“ Modelle betrieben und u.a. für verschiedene Sensitivitätsexperiment benutzt. Diese zeigten, dass die Modellergebnisse von der Güte und konkreten Spezifikation des jeweiligen Randes (d.h. der Vorgabe des oberen Randes beim stand-alone Ozean-Meereismodell bzw. des unteren Randes beim stand-alone Atmosphärenmodell) abhängen. Ergebnisse des stand-alone Ozean-Meereismodells NAOSIM zeigen den dominierenden Einfluss des atmosphärischen Antriebs auf die Simulation von Meereisanomalien (Kauker et al., 2003). Andererseits weisen Sensitivitätsstudien mit dem stand-alone Atmosphärenmodell HIRHAM darauf hin, dass die großskalige atmosphärische Zirkulation durch das Modell nur bei akkurat vorgegebenen Meereisdaten reproduziert werden kann (Rinke et al., 2003, 2006).
Daraus kann man ableiten, dass in der Realität komplexe Wechselwirkungen und Rückkopplungen zwischen Atmosphäre und Ozean-Meereis ablaufen, die nur in dem gekoppelten Atmosphäre-Ozean-Meereis-Modellsystem berücksichtigt werden können. Um im gekoppelten Modell eine realistische sommerliche Meereisbedeckung zu erhalten, ist es einerseits notwendig, die atmosphärische Zirkulation (d.h. das Bodenluftdruckfeld) und den atmosphärischen Zustand (d.h. die Lufttemperatur, Wolkenbedeckung, usw.) in den Sommermonaten realistisch zu reproduzieren, denn diese Faktoren beeinflussen die Meereisdrift und die Rate des Schmelzen. Für letzteres spielt die Eis-Albedo-Rückkopplung eine zentrale Rolle (Dorn et al., 2009). Andererseits ist es genau so wichtig, die Meereisdickenverteilung im davorliegenden Frühjahr realistisch zu simulieren, wobei dies wiederum von der Meereisentwicklung in den vorhergehenden Jahren abhängt (Dorn et al., 2012). Das gekoppelte Modell ermöglicht es ausserdem zu untersuchen, inwieweit Meereisanomalien in verschiedenen Regionen des arktischen Ozeans auf die atmosphärischen Zirkulation verschiedenartig rückkoppeln können. Rinke et al. (2013) konnten zeigten, dass die Barents-/Kara und Beaufort Seen sehr sensitive Regionen sind, da dort auftretende sommerliche Meereisanomalien starke atmosphärische Rückkopplungen im folgenden Herbst/Winter erzeugen.
Dr. Annette Rinke
Alfred-Wegener-Institut Helmholtz-Zentrum für Polar- und Meeresforschung (AWI), Potsdam
- Christensen, J. H., Christensen, O. B., Lopez, P., van Meijgaard, E., and Botzet, M., 1996.: The HIRHAM4 regional atmospheric climate model, DMI Sci. Rep. 96–4, Dan. Meteorol. Inst., Copenhagen, Denmark, 51 pp
- Dethloff, K., A. Rinke, R. Lehmann, J. H. Christensen, M. Botzet, B. Machenhauer, 1996: Regional climate model of the Arctic atmosphere. J. Geophys. Res. 101, 23401-23422
- Dorn, W., K. Dethloff, A. Rinke, S. Frickenhaus, R. Gerdes, M. Karcher, and F. Kauker, 2007: Sensitivities and uncertainties in a coupled regional atmosphere-ocean-ice model with respect to the simulation of Arctic sea-ice, J. Geophys. Res. 112, D10118, doi:10.1029/2006JD007814
- Dorn, W., Dethloff, K., and Rinke, A, 2009.: Improved simulation of feedbacks between atmosphere and sea ice over the Arctic Ocean in a coupled regional climate model, Ocean Model., 29, 103–114, doi:10.1016/j.ocemod.2009.03.010
- Dorn, W., K. Dethloff, and A. Rinke, 2012: Limitations of a coupled regional climate model in the reproduction of the observed Arctic sea-ice retreat, The Cryosphere Discuss., 6, 1269-1306, doi:10.5194/tcd-6-1269-2012
- Gustafsson, N., 1993: HIRLAM 2 Final Report., HIRLAM techn. Report, Norrköping
- Hibler, W. D., III, 1979: A dynamic thermodynamic sea ice model, J. Phys. Oceanogr., 9, 815– 846
- Hunke, E. C., and J. K. Dukowicz, 1997: An elastic-viscous-plastic model for sea ice dynamics, J. Phys. Oceanogr., 27, 1849–1867
- Kalnay, E., Kanamitsu, M., Kistler, R., Collins, W., Deaven, D., Gandin, L., Iredell, M., Saha, S., White, G., Woollen, J., Zhu, Y., Leetmaa, A., Reynolds, R., Chelliah, M., Ebisuzaki, W., Higgins, W., Janowiak, J., Mo, K. C., Ropelewski, C., Wang, J., Jenne, R., and Joseph, D., 1996: The NCEP/NCAR 40-year reanalysis project, B. Am. Meteorol. Soc., 77, 437-471
- Köberle, C. and Gerdes, R. (2007): Simulated variability of the Arctic Ocean fresh water balance 1948-2001, J. Phys. Oceanogr., 37 (6), 1628-1644, doi: 10.1175/JPO3063.1
- Lemke, P., W. D. Hibler, G. Flato, M. Harder, and M. Kreyscher, 1997: On the improvement of sea ice models for climate simulations: The Sea Ice Model Intercomparison Project, Ann. Glaciol., 25, 183– 187
- Machenhauer, B., 1988: The HIRLAM final report, HIRLAM Technical Report 5, Danish Meteorological Institute, Copenhagen, Denmark
- Matthes, H., A. Rinke, P. Miller, P. Kuhry, and K. Dethloff, 2011: Sensitivity of high-resolution Arctic regional climate model projections to different implementations of land surface processes, Clim. Change, doi:10.1007/s10584-011-0138-1
- Pacanowski, R.C., 1996: MOM 2 documentation, user’s guide and reference manual, GFDL Ocean Tech. Rep. 3.2, 329 pp., Geophys. Fluid Dyn. Lab., Princeton Univ. Press, Princeton, N. J.
- Rinke, A., R.Gerdes, K. Dethloff, T. Kandlbinder, M.Karcher, F. Kauker, S.Frickenhaus, C. Koeberle, W.Hiller, 2003: A case study of the anomalous Arctic sea ice conditions during 1990: Insights from coupled and uncoupled regional climate model simulations, J.Geo¬phys. Res. 108, 4275, doi:10.1029/2002JD003146
- Rinke, A., W. Maslowski, K. Dethloff, and J. Clement, 2006: Influence of sea ice on the atmosphere: A study with an Arctic atmospheric regional climate model, J. Geophys. Res., 111, D16103, doi:10.1029/2005JD006957
- Rinke, A., P. Kuhry, and K. Dethloff, 2008: Importance of a soil organic layer for Arctic climate: a sensitivity study with an Arctic RCM, Geophys. Res. Lett. 35, L13709, doi:10.1029/2008GL034052
- Rinke, A., K. Dethloff, W. Dorn, D. Handorf, and J.C. Moore, 2013: Simulated Arctic atmospheric feedbacks associated with late summer sea ice anomalies, J. Geophys. Res., 118, 7698–7714, doi:10.1002/jgrd.50584
- Roeckner, E., Arpe, K., Bengtsson, L., Christoph, M., Claussen, M., Dümenil, L., Esch, M., Giorgetta, M., Schlese, U., Schulzweida, U., 1996: The atmospheric general circulation model ECHAM-4: model description and simulation of present-day climate. MPI Rep. 218, Max Planck Inst. for Meteorol., Hamburg, Germany, 90pp
- Roeckner, E; Bäuml, G; Bonaventura, L; Brokopf, R; Esch, M; Giorgetta, M; Hagemann, S; Kirchner, I; Kornblueh, L; Manzini, E; Rhodin, A; Schlese, U; Schulzweida, U; and Tompkins, A., 2003: The atmospheric general circulation model ECHAM5. Part 1. Model description. Report No. 349, Max-Planck-Institut für Meteorologie
- Semtner, A. J., Jr., 1976: Model for the thermodynamic growth of sea ice in numerical investigations of climate, J. Phys. Oceanogr., 6, 379–389